[0281] Na praia ou na montanha: cinco teoremas que ajudam a resolver o Kakuro

As regras do Kakuro são muito simples (ver a mensagem «0182»). Consoante a dimensão escolhida, a sua resolução pode demorar entre alguns minutos e duas ou três dezenas de minutos.

E há sempre novos casos disponíveis, por exemplo em https://www.kakuros.com/.

As ferramentas mestras para a resolução de um Kakuro são a lógica e a combinatória. Mas elas aliam-se de diversas formas para ir resolvendo cada caso. Podemos chamar teoremas a essas alianças.

Um dos mais simples pode ser chamado teorema do cruzamento do «7 + 9» com o «8 + 9».
O cruzamento referido junta a «soma 16 com duas parcelas» (que só pode resultar de «7 + 9») e a «soma 17 com duas parcelas» (inescapavelmente resultante de «8 + 9»).
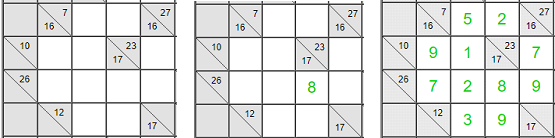
Na figura seguinte mostra-se, primeiro, um desses cruzamentos; depois a óbvia solução (o «9» é o único número comum às duas somas); e, por fim, as consequências práticas que se podem tirar deste cruzamento:

Com estas mesmas características há o teorema do cruzamento do «1 + 2» com o «1 + 3», sendo o «1» a respectiva solução.

Ligeiramente mais exigente é o teorema do número mínimo exigido e igual ao número máximo disponível.
Na figura, a «soma 3» só proporciona as parcelas «1 + 2»; ora a parcela «1» é insuficiente (pois as outras duas parcelas não podem somar «18»), pelo que é forçoso usar a parcela «2». O que, neste caso, permite deduzir vários outros números nas redondezas:

O teorema duas vezes «7 + 9» mais uma vez «8 + 9» pode passar desapercebido aos mais inexperientes.
Na figura, a «soma 26» cruza duas somas «7 + 9» e uma soma «8 + 9». Como estas três somas só podem ser constituídas pelas parcelas «7», «8» e «9», então a «soma 26» tem de as incluir, sendo a parcela «8» apenas atribuível à «soma 17». Tendo-a escrita, é possível, por dedução e experimentação, chegar a bastantes mais números situados nas proximidades:

São semelhantes a este o teorema uma vez «7 + 9» mais duas vezes «8 + 9», o teorema duas vezes «1 + 2» mais uma vez «1 + 3» e o teorema uma vez «1 + 2» mais duas vezes 1 + 3».

O teorema das N parcelas ladeadas por N + 1 parcelas é particularmente subtil.
Na figura, a «soma 17» (3 parcelas) está ladeada pela «soma 26» (4 parcelas). Então, estas sete parcelas somarão «43». Se subtrairmos a «43» as três somas verticais, «16», «3» e «17», restará «7», que só pode ser a parcela mais à direita!

A aplicação do teorema das parcelas pré-definidas está normalmente associada à mobilização de outros teoremas.
No exemplo figurado, a «soma 37» é atravessada pelas somas «24», «23», «17» e «16». Ora estas somas são exclusivamente constituídas pelas parcelas «6», «7», «8» e «9». Então estes números terão de figurar na «soma 37», garantindo-lhe uma «sub soma 30». Pelo que as somas «7», «3» e «6» terão de contribuir com a «sub soma 7». Ora cada uma destas somas resulta de uma combinação única de parcelas, respectivamente «1 + 2 + 4», «1 + 2» e «1 + 2 + 3»). Pensando um pouco, a parcela «4» só pode estar incluída na «soma 7».
Depois, na «soma 19» situada mais acima (existe outra mais abaixo), é exigido que figure a parcela «2» (de acordo o segundo teorema). A partir daqui muitos outros números nas proximidades se deduzem com facilidade: