[0272] O tabuleiro de Galton

Muitos dos que já assistiram a concursos televisivos se lembrarão de ver um tabuleiro, colocado verticalmente ou com uma pequena inclinação, guarnecido na sua parte central com um conjunto de pinos dispostos triangularmente. Chegado o momento de ser usado, eram-lhe introduzidas sucessivas bolas no topo; e estas, ao caírem, desviavam-se ou para a esquerda ou para a direita ao embaterem nos pinos, até que se alojavam num dos receptáculos dispostos ao longo da base:

Um tabuleiro assim chama-se Tabuleiro de Galton.

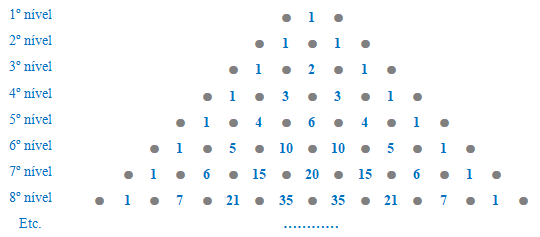
A construção destes tabuleiros deve assegurar que as bolas têm a mesma probabilidade de se desviarem para um ou outro lado de cada pino ao embaterem nele. Sendo assim, a proporção teórica das bolas que passarão nos sucessivos níveis de pinos é a seguinte:

Por exemplo no 4ª nível, a proporção teórica, para cada 8 bolas lançadas, é de 1 bola nos dois intervalos extremos e de 3 bolas em cada um dos intervalos centrais.
Este triângulo de números, encaixado no interior do triângulo de pinos, é chamado Triângulo de Pascal. E os números de cada nível correspondem aos coeficientes do desenvolvimento do chamado Binómio de Newton, (a + b) ⁿ, correspondendo o 1º nível a n = 0, o 2º nível a n = 1, e assim sucessivamente.
Francis Galton (1822 - 1911), o inventor deste tabuleiro, juntou num só instrumento manipulável as contribuições de dois matemáticos de peso. E, através dele, exemplificou aquilo a que hoje se chama, em Estatística, uma distribuição binomial.

 

Lembrei-me deste tabuleiro quando passeava numa praia ao longo da maré baixa. A água tinha escorrido devagar, em direcção ao mar, e formara o padrão que se vê nesta fotografia:

Podemos imaginar que existem pinos dispostos triangularmente. Mas observamos que não há uma maior acumulação de «bolas» no «centro» da chegada. É que neste «tabuleiro» as «bolas» não descem a partir de um só ponto, mas de todos os pontos de um topo tão longo quanto a linha chegada. A distribuição estatística das gotas de água que deslizam para o mar é, portanto, uniforme.

 

Fonte: livro de Cundy & Rollet (1989; pp. 217-219)
Fotografia: Eva Maria Blum